Response Spectrum Analysis
Author: Win Aung Cho18-Apr-2022 07:04:13 PM*
☞ RHA (Response history analysis)
ငလျင်တခုအတွက် ၎င်းငလျင်လှုပ်သည့်အတိုင်း အရွေ့တခုသာရှိသည့် (SDOF) စိတ်ကူးယဥ် အဆောက်အဦ ကိုဆက်တိုက် လှုပ်ရှားစေပါမည်၊ အချိန်တိုင်းအတွက် ရွေ့လျားမှုများကို တွက်ထုတ်ပါမည်၊ အမြင့်ဆုံး ရွေ့လျားတုံ့ပြန်မှု (အရွေ့၊ အလျင်၊ အရှိန်) (Maximum responses) များကိုမှတ်သားပါမည်။
SDOF System
စိတ်ကူးယဥ် အဆောက်အဦ ၏ ဂုဏ်သတ္တိ အချက်အလက်များမှာ
၁ ဒြပ်ထု (M=Mass)
၂ ခုခံအားတောင့်တင်းမှု (K=Stiffness)
၃ ရွေ့လျားမှုကို ဟန့်တားနိုင်မှု (C=Dumping)
၄ တုန်ခါမှု နှုန်းကိန်းသေ (ω = radian per second)
၅ ရွေ့လျားမှုကို ဟန့်တားသည့် အချိုးကိန်းသေ (ξ = dumping ratio)
ω သည် M နှင့် K ပေါ်မူတည်သည့် ကိန်းသေဖြစ်ပြီး တုံခါချိန် လွှဲခွင် (T=2π⁄ω natural period) အဖြစ်လည်း ဖေါ်ပြပါသည်၊
ξ သည် M နှင့် K ပေါ်မူတည်သည့် တုံခါမှုအခြေအနေကို ကန့်သတ်သည့် Cc နှင့် C ၏ အချိုးဖြစ်သည်)
ငလျင်၏ အချက်အလက်မှာ
၁ üg(t) မြေပြင်ရွေ့လျားမှု အရှိန်
အဆောက်အဦ၏ တုံ့ပြန်မှု (building responses)
၁ အရွေ့ u(t)
၂ အလျင် u̇(t)
၃ အရှိန် ü(t)
အမြင့်ဆုံး ရွေ့လျားတုံ့ပြန်မှု (အရွေ့၊ အလျင်၊ အရှိန်) (Maximum responses) များကို အမျိုးမျိုးသော T နှင့် ξ များအတွက် ရှာ၍ ဇယားဖြင့်၎င်း ၃မျိုးပုံပြဂရပ်ဖ် (အရွေ့ အလျင် အရှိန် Tripertite ) ဖြင့်၎င်း တမျိုးပုံပြဂရပ် (အရှိန် response spectrum) ဖြင့်၎င်း ပြကြသည်။
RHS မှရသော (response spectrum) ဂရဖ် သည် ငလျင်တခု၏ accelerogram မှရခြင်းဖြစ်သည်၊ အဖြေကို ငလျင်လှုပ်ရာတွင်တိုင်းသည့် အချိန်အကွာအဝေး (ဥပမာ ၀.၀၂ စက္ကန့်ခြား) အလိုက်တွက်ချက်ထားသဖြင့် အဖြများသည် အပြောင်းအလည်မြန်ဆန်ပြီး မိမိအဆောက်အဦ ၏ T အတွက် ခန့်မှန်း တုန့်ပြန် အရှိန် ယူရန် လွဲ မှားနိုင်သည်၊ သို့ဖြစ်၍ ငလျင်တိုင်းတာသည့် အချိန်အကွာအဝေးထက် ပိုမိုခြားနားစေလျက် ပျမ်းမျှယူ၍ တွက်ချက်လေ့ရှိသည်။ ၎င်း ဂရဖ်ကို အသုံးပြု၍ အဆောက်အဦ ဒီဇိုင်းတွက်ချက်ရာတွင် အသုံးပြုနိုင်သည်၊ အသုံးပြုသော accelerogram သည် ဒီဇိုင်းတွက်ချက်မည့် အဆောက်အဦ တည်နေရာ၌ ဖြစ်လျင်ပိုကောင်းသည်။
ငလျင်တခုအတွက် ၎င်းငလျင်လှုပ်သည့်အတိုင်း အရွေ့တခုသာရှိသည့် (SDOF) စိတ်ကူးယဥ် အဆောက်အဦ ကိုဆက်တိုက် လှုပ်ရှားစေပါမည်၊ အချိန်တိုင်းအတွက် ရွေ့လျားမှုများကို တွက်ထုတ်ပါမည်၊ အမြင့်ဆုံး ရွေ့လျားတုံ့ပြန်မှု (အရွေ့၊ အလျင်၊ အရှိန်) (Maximum responses) များကိုမှတ်သားပါမည်။
SDOF System
စိတ်ကူးယဥ် အဆောက်အဦ ၏ ဂုဏ်သတ္တိ အချက်အလက်များမှာ
၁ ဒြပ်ထု (M=Mass)
၂ ခုခံအားတောင့်တင်းမှု (K=Stiffness)
၃ ရွေ့လျားမှုကို ဟန့်တားနိုင်မှု (C=Dumping)
၄ တုန်ခါမှု နှုန်းကိန်းသေ (ω = radian per second)
၅ ရွေ့လျားမှုကို ဟန့်တားသည့် အချိုးကိန်းသေ (ξ = dumping ratio)
ω သည် M နှင့် K ပေါ်မူတည်သည့် ကိန်းသေဖြစ်ပြီး တုံခါချိန် လွှဲခွင် (T=2π⁄ω natural period) အဖြစ်လည်း ဖေါ်ပြပါသည်၊
ξ သည် M နှင့် K ပေါ်မူတည်သည့် တုံခါမှုအခြေအနေကို ကန့်သတ်သည့် Cc နှင့် C ၏ အချိုးဖြစ်သည်)
ငလျင်၏ အချက်အလက်မှာ
၁ üg(t) မြေပြင်ရွေ့လျားမှု အရှိန်
အဆောက်အဦ၏ တုံ့ပြန်မှု (building responses)
၁ အရွေ့ u(t)
၂ အလျင် u̇(t)
၃ အရှိန် ü(t)
အမြင့်ဆုံး ရွေ့လျားတုံ့ပြန်မှု (အရွေ့၊ အလျင်၊ အရှိန်) (Maximum responses) များကို အမျိုးမျိုးသော T နှင့် ξ များအတွက် ရှာ၍ ဇယားဖြင့်၎င်း ၃မျိုးပုံပြဂရပ်ဖ် (အရွေ့ အလျင် အရှိန် Tripertite ) ဖြင့်၎င်း တမျိုးပုံပြဂရပ် (အရှိန် response spectrum) ဖြင့်၎င်း ပြကြသည်။
RHS မှရသော (response spectrum) ဂရဖ် သည် ငလျင်တခု၏ accelerogram မှရခြင်းဖြစ်သည်၊ အဖြေကို ငလျင်လှုပ်ရာတွင်တိုင်းသည့် အချိန်အကွာအဝေး (ဥပမာ ၀.၀၂ စက္ကန့်ခြား) အလိုက်တွက်ချက်ထားသဖြင့် အဖြများသည် အပြောင်းအလည်မြန်ဆန်ပြီး မိမိအဆောက်အဦ ၏ T အတွက် ခန့်မှန်း တုန့်ပြန် အရှိန် ယူရန် လွဲ မှားနိုင်သည်၊ သို့ဖြစ်၍ ငလျင်တိုင်းတာသည့် အချိန်အကွာအဝေးထက် ပိုမိုခြားနားစေလျက် ပျမ်းမျှယူ၍ တွက်ချက်လေ့ရှိသည်။ ၎င်း ဂရဖ်ကို အသုံးပြု၍ အဆောက်အဦ ဒီဇိုင်းတွက်ချက်ရာတွင် အသုံးပြုနိုင်သည်၊ အသုံးပြုသော accelerogram သည် ဒီဇိုင်းတွက်ချက်မည့် အဆောက်အဦ တည်နေရာ၌ ဖြစ်လျင်ပိုကောင်းသည်။

Single Degree of Freedom Structure
☞ Design response spectrum
ပြီးခဲ့သော နှစ်ပေါင်း ၅၀ နှင့် ဖြစ်နိုင်ဆုံးသော ငလျင်များ မှတုံ့ပြန်မှုများကို အဆောက်အဦ အမျိုးအစားအလိုက် (ဥပမာ သံထည်၊ သစ်သား၊ ကွန်ကရိ၊ ဂိုထောင်၊ စက်ရုံ၊ တံတား၊ မျှော်စင်) ဆောက်လုပ်ပုံစံနစ်၊ အောက်ခံ မြေအမျိုးအစား၊ စသည်တို့ကို စဥ်းစား တွက်ချက်၍ အနီးစပ်ဆုံး ဖြစ်နိုင်သည့် (response spectrum) များကို တွက်ချက်ရသည်။ များသောအားဖြင့် သုတေသန စာတမ်းများမှ ထုတ်ပေးထားသော သင်္ချာပုံစံများ ကို ကိုးကား၍ response spectrum ၏ အချက်အလက်များကို ပြင်ဆင်ယူရသည်။
Short and Long period building
နိမ့်၍ ဗျက်ကျယ်သော အဆောက်အဦများသည် (လွှဲခွင်နိမ့်) short period building များဖြစ်၍ မြင့်ပြီး ဗျက်ကျဥ်းသော အဆောက်အဦများသည် (လွှဲခွင်မြင့်) long period building များဖြစ်ကြသည်၊
အဆောက်အဦ၏ အခြေခံ တုံခါကြာချိန် T (fundamental natural period)
ကိုအခြေခံ ၍သတ်မှတ်ခြင်း ဖြစ်သည်၊ အဆောက်အဦ တုံခါသောအခါ အသွားအပြန် တခေါက် ရွေ့လျားတုံခါရန် ကြာချိန်ကို T ဖြင့်သတ်မှတ်သည်၊ စက္ကန့် ဖြစ်သည်၊ အထက်အောက် အလွှာလိုက် တည်ဆောက်ထားသော multi story building တခုတွင် တလွှာတက်သွားတိုင်း လွှဲခွင်ကြာချိန် ၀.၁ စက္ကန့် တိုးသည်ဟု ခန့်မှန်းနိုင်သည်၊ ထို့ကြောင့် ၆ထပ်အဆောက်အဦ၏ T သည် 0.6s ခန့်ဖြစ်၍ ၁၀ ထပ် အဆောက်အဦသည် T = 1s ခန့်ဖြစ်သည်။
လွှဲချိန် T 0.35s ထက်နဲသော အဆောက်အဦများတွင် အရွေ့ကြောင့်ဖြစ်သော အားသည် အဓိကဖြစ်သည်၊ (displacement control) T 0.35s နှင့် 3.5 s ကြားရှိသော အဆောက်အဦများတွင် ရွေ့လျားအလျင် မှဖြစ်သော အားသည် အဓိကဖြစ်သည်၊ (velocity control)
ပြီးခဲ့သော နှစ်ပေါင်း ၅၀ နှင့် ဖြစ်နိုင်ဆုံးသော ငလျင်များ မှတုံ့ပြန်မှုများကို အဆောက်အဦ အမျိုးအစားအလိုက် (ဥပမာ သံထည်၊ သစ်သား၊ ကွန်ကရိ၊ ဂိုထောင်၊ စက်ရုံ၊ တံတား၊ မျှော်စင်) ဆောက်လုပ်ပုံစံနစ်၊ အောက်ခံ မြေအမျိုးအစား၊ စသည်တို့ကို စဥ်းစား တွက်ချက်၍ အနီးစပ်ဆုံး ဖြစ်နိုင်သည့် (response spectrum) များကို တွက်ချက်ရသည်။ များသောအားဖြင့် သုတေသန စာတမ်းများမှ ထုတ်ပေးထားသော သင်္ချာပုံစံများ ကို ကိုးကား၍ response spectrum ၏ အချက်အလက်များကို ပြင်ဆင်ယူရသည်။
Short and Long period building
နိမ့်၍ ဗျက်ကျယ်သော အဆောက်အဦများသည် (လွှဲခွင်နိမ့်) short period building များဖြစ်၍ မြင့်ပြီး ဗျက်ကျဥ်းသော အဆောက်အဦများသည် (လွှဲခွင်မြင့်) long period building များဖြစ်ကြသည်၊
အဆောက်အဦ၏ အခြေခံ တုံခါကြာချိန် T (fundamental natural period)
ကိုအခြေခံ ၍သတ်မှတ်ခြင်း ဖြစ်သည်၊ အဆောက်အဦ တုံခါသောအခါ အသွားအပြန် တခေါက် ရွေ့လျားတုံခါရန် ကြာချိန်ကို T ဖြင့်သတ်မှတ်သည်၊ စက္ကန့် ဖြစ်သည်၊ အထက်အောက် အလွှာလိုက် တည်ဆောက်ထားသော multi story building တခုတွင် တလွှာတက်သွားတိုင်း လွှဲခွင်ကြာချိန် ၀.၁ စက္ကန့် တိုးသည်ဟု ခန့်မှန်းနိုင်သည်၊ ထို့ကြောင့် ၆ထပ်အဆောက်အဦ၏ T သည် 0.6s ခန့်ဖြစ်၍ ၁၀ ထပ် အဆောက်အဦသည် T = 1s ခန့်ဖြစ်သည်။
လွှဲချိန် T 0.35s ထက်နဲသော အဆောက်အဦများတွင် အရွေ့ကြောင့်ဖြစ်သော အားသည် အဓိကဖြစ်သည်၊ (displacement control) T 0.35s နှင့် 3.5 s ကြားရှိသော အဆောက်အဦများတွင် ရွေ့လျားအလျင် မှဖြစ်သော အားသည် အဓိကဖြစ်သည်၊ (velocity control)

Respinse History Analysis
☞ Response spectrum defined by CODE
၎င်းနောက် ပိုမိုလွယ်ကူ ရှင်းလင်း၍ ဒီဇိုင်နာ ကိုယ်တိုင် (accelerogram မရှိဘဲ) response spectrum graph တည်ဆောက်နိုင်ရန် ကိန်းသေများ သတ်မှတ်ပေးကြသည်။ ထိုသို့တည်ဆောက်နိုင်ရန် RHS ကို SDOF System structure ၃ မျိုးခွဲခြားရသည်၊ တခုမှာ T ၁ စက္ကန့် အတွက်ဖြစ်ပြီး၊ နောက်တခုမှာ T ၀.၆ (short period) စက္ကန့် နှင့် အခြားသော T တန်ဘိုးများ (Long period) အတွက် ဖြစ်သည်။
နောက်ဆုံးရရှိသော ဂရပ်ဖ်မှာ design response spectrum graph ဖြစ်ပြီး ၎င်းတွင်သတ်မှတ်သော 1s period နှင့် short period response (0.6s) acceleration များကို ဇယားများဖြင့် ဖေါ်ပြကြသည်။
အဆောက်အဦ၊ မြေအမျိုးအစား နှင့် ပါတ်သက်သော ကိန်းသေများဖြင့်ပေါင်းစပ်၍ design response spectrum graph ကို ရေးဆွဲကာ မိမိတည်ဆောက်မည့် အဆောက်အဦ၏ T သဘာဝတုံခါမှု လွှဲခွင်နှင့် သင့်လျော်သော တုံ့ပြန်မှုကို ရရှိပါမည်။
ထိုမှတဆင့် ထိုတုံပြန်မှု အရွေ့ အရှိန် နှင့် အလျင်များကို ခံနိုင်ရည်ရှိသော အဆောက်အဦကို ဒီဇိုင်းပြုတွက်ချက်နိုင်ကြပေမည်။
၎င်းနောက် ပိုမိုလွယ်ကူ ရှင်းလင်း၍ ဒီဇိုင်နာ ကိုယ်တိုင် (accelerogram မရှိဘဲ) response spectrum graph တည်ဆောက်နိုင်ရန် ကိန်းသေများ သတ်မှတ်ပေးကြသည်။ ထိုသို့တည်ဆောက်နိုင်ရန် RHS ကို SDOF System structure ၃ မျိုးခွဲခြားရသည်၊ တခုမှာ T ၁ စက္ကန့် အတွက်ဖြစ်ပြီး၊ နောက်တခုမှာ T ၀.၆ (short period) စက္ကန့် နှင့် အခြားသော T တန်ဘိုးများ (Long period) အတွက် ဖြစ်သည်။
နောက်ဆုံးရရှိသော ဂရပ်ဖ်မှာ design response spectrum graph ဖြစ်ပြီး ၎င်းတွင်သတ်မှတ်သော 1s period နှင့် short period response (0.6s) acceleration များကို ဇယားများဖြင့် ဖေါ်ပြကြသည်။
အဆောက်အဦ၊ မြေအမျိုးအစား နှင့် ပါတ်သက်သော ကိန်းသေများဖြင့်ပေါင်းစပ်၍ design response spectrum graph ကို ရေးဆွဲကာ မိမိတည်ဆောက်မည့် အဆောက်အဦ၏ T သဘာဝတုံခါမှု လွှဲခွင်နှင့် သင့်လျော်သော တုံ့ပြန်မှုကို ရရှိပါမည်။
ထိုမှတဆင့် ထိုတုံပြန်မှု အရွေ့ အရှိန် နှင့် အလျင်များကို ခံနိုင်ရည်ရှိသော အဆောက်အဦကို ဒီဇိုင်းပြုတွက်ချက်နိုင်ကြပေမည်။
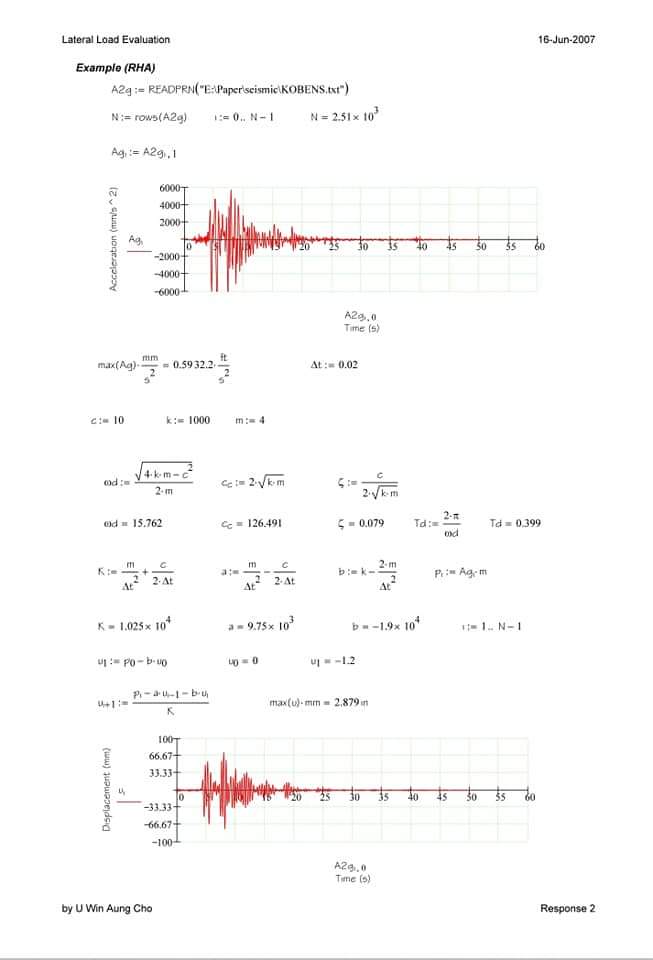
RHA by using Central Difference Method
☞ PHP CODE for Response Spectrum Analysis
<?php $PI = +3.1415; $DT = 0.02; $accgraphname = "kobens.txt"; $C = 10; $K=1000; $M = 4; $i=0; $Ag = array(); if (file_exists($accgraphname)){ $lines = file($accgraphname); foreach($lines as $line){ $line = trim($line); if (!empty($line)){ list($dt, $ac) = explode(",", $line); $Ag[$i] = $ac; $i++; } } } $wd = sqrt(4*$K*$M-$C*$C)/(2*$M); $Cc = 2*sqrt($K*$M); $zi = $C/$Cc; $Td = 2*$PI/$wd; //$wd = sqrt(4*$K*$M-($zi*$zi*4*$K*$M))/(2*$M); //$wd = sqrt($K/$M*(1-$zi*$zi)); //$wd*$wd/(1-$zi*$zi) = $K/$M; $k = $M/($DT*$DT)+$C/(2*$DT); $a = $M/($DT*$DT)-$C/(2*$DT); $b = $K-2*$M/($DT*$DT); $p = array(); while($val = each($Ag)){ $p[] = $val[1]*$M; } $u[0] = 0; $u[1] = $p[0]-$b*$u[0]; $n = count($Ag); $umin=$umax=0; for ($i=1; $i<$n; $i++) { $u[$i+1] = ($p[$i]-$a*$u[$i-1]-$b*$u[$i])/$k; if ($umin > $u[$i+1]) $umin = $u[$i+1]; if ($umax < $u[$i+1]) $umax = $u[$i+1]; }; $imgfile = "xydata.txt"; $imgw = 680; $imgh = 200; $mgleft = $mgright = $mgtop = $mgbot = 20; $x0 = 10; $y0 = ($imgh-$mgtop-$mgbot)/2; $scx = 20; $scy = 1; $ngx = 10; $ngy = 4; $fp = fopen($imgfile, "w"); if ($fp){ fputs($fp, "$imgw|$imgh|$mgleft|$mgright|$mgtop|$mgbot|$x0|$y0|$scx|$scy|$ngx|$ngy\r\n"); fputs($fp, "$DT|$n\r\n"); fputs($fp, "$u[0]"); for ($i=1; $i<$n; $i++) { fputs($fp, ",$u[$i]"); } fclose($fp); } echo "<img src=\"xygraph.php?fname=$imgfile\">"; echo "<table>"; echo "<tr><th>Period</th><td>$Td</td><td>sec</td></tr>"; echo "<tr><th>Dumping ratio</th><td>$zi</td><td></td></tr>"; echo "<tr><th>Max U</th><td>$umax</td><td></td></tr>"; echo "<tr><th>Min U</th><td>$umin</td><td></td></tr>"; echo "<tr><th>Cc</th><td>$Cc</td><td></td></tr>"; echo "</table>"; ?>
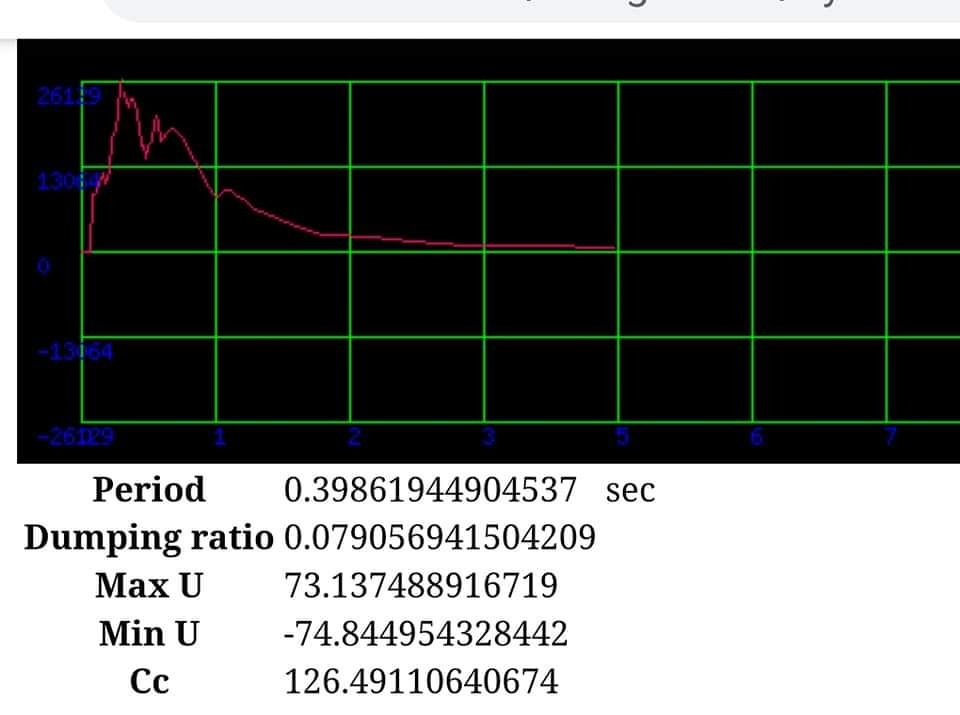
Response Spectrum Analysis
Author: Win Aung Cho
18-Apr-2022 07:04:13 PM*